Design

The two main classes in the project are the singletons Rosters and RosterSolver. Rosters holds all the data and acts as a document class and RosterSolver implements the puzzling algorithm. The puzzling algorithm is an evolutionary algorithm. All the subjects are assigned sequentially. The puzzling algorithm works in two stages: first all the solutions (that take less than a preset number of steps) for adding one subject are sought, then each solution gets a score and the one with the highest score is used.

Actors

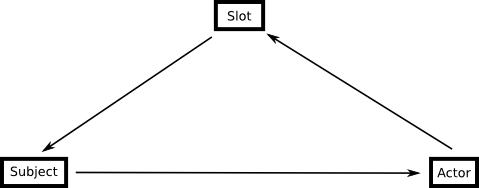
Instead of treating classes and teachers seperately they are both represented by the Actor class. A prototype implementation showed strong similarity in the algorithm of those two, so using a single Actor class simplefies things. Also, sometimes class rooms like the physics room need to be linked with a subject, this link can also be represented by an Actor. So a Subject can have any number of actors.

Representation of a roster

The evident choice to represent a roster is as an ArrayList of days and for each day an ArrayList of slots. However this complicates the algorithm in two ways: the ArrayLists of slots can be of different lengths and to iterate over the slots two loops are needed. It is better to combine the day and slot index into a SlotIndex class and then store the roster as an HashMap of SlotIndex versus Slot. The Rosters singelton holds an ArrayList of all used SlotIndices to facilitate the iteration.

In the HashMap an empty slot isn't stored, so the slots HashMap only holds keys for slots that are actually filled in.

You might think that the Slot class isn't needed and that we could just as well use a HashMap of SlotIndex versus Subject but this isn't true. A slot can also contain a tag, this is an element that is assigned by a prefilled roster and can't be moved.

Ownership of the rosters

Each Actor has a HashMap of Slots, Slots can contain Subjects, and each Subject has a list of Actors that are involved in the subject. It is this loop over which the puzzling algorithm iterates to assign and move subjects.

Finding solutions

The main loop of the algorithm iterates over all the subjects that need to be assigned, assigning each one to a slot as it goes along. To assign a subject, a second loop iterates over the available SlotIndices. Each SlotIndex is considered as a place to put the subject. If the SlotIndex is already used by one of the Actors, the Subject at that place is marked to be moved. SlotIndices are skipped if one of the following conditions is true:

The index is the original position of the subject (for a subject that is being moved, not assigned).
A Subject is already being moved to that index for one of the Actors.
The slot isn't moveable for one of the actors.
An Actor already holds an equivalent Subject at that index.

For each SlotIndex that isn't skipped a SubjectSolution is created that holds the movement of the Subject to the SlotIndex as the first step. Also a list of all the Subjects that need to be moved is composed. For each of these Subjects a new position is sought by again iterating over all the SlotIndices, and these steps are again added to the SubjectSolution. This process is continued until one of two conditions are met:

The number of steps exceeds a preset number, in this case the solution is rejected
There are no more Subjects that need to be moved, in this case the solution is added to the list of possible solutions

Scoring the solutions

Solutions are scored in three ways. After each score is calculated the highest scoring solutions are filtered out and with the remaining solutions the next way of scoring is calculated.

Spread/group score

The first way that solutions are scored is by their position in the roster. Each subject that has a count that is greater than one can have a spread or group scoring strategy. With spread scoring the score is higher if the subjects are spread out over the week. With group scoring the score is higher if the subjects are grouped together in blocks.

Cluster score

Sometimes subjects are grouped in clusters. When you have 4 actors A, B, C and D and 4 subjects S1, S2, S3 and S4 that are linked as follows. A and B are linked with S1, C and D are linked with S2, A and C are linked with S3 and B and D are linked with S4. Then S1 and S2 form a cluster because they have to be thought parallel to each other. And S3 and S4 form a cluster.

For all the assigned subjects the cluster score of the solution is increased if the subjects of the solution have the same cluster id and index as the assigned subject. This means that the assigned subject needs to be parallel to the subject of the solution. For all the unassigned subjects with the same cluster id as the solution subject it is checked if the subject can be placed at the index of the solution subject, if not the score is reset.

Unmoveable conflicts

An unmoveable conflict occurs when an actor has x subjects of a cluster with y subjects and more than (y - x) subjects of that cluster are placed in slots that are unmoveable for that actor.

If all the unmoveable places are filled with a subject, the unmoveable conflicts score is decremented. If the cluster id of the subject equals the cluster id where there is the least chance for an unmoveable conflict to occur the unmoveable conflicts score is incremented.